Draw a Circle Without Floating Point Arithmetic C

next → ← prev

Bresenham's Line Algorithm

This algorithm is used for browse converting a line. It was developed by Bresenham. It is an efficient method considering information technology involves simply integer addition, subtractions, and multiplication operations. These operations can be performed very quickly so lines tin be generated quickly.

In this method, next pixel selected is that i who has the least altitude from true line.

The method works every bit follows:

Assume a pixel P_i'(x₁',y₁'),then select subsequent pixels as we work our may to the dark, one pixel position at a time in the horizontal direction toward P₂'(x₂',y₂').

Once a pixel in choose at whatever step

The next pixel is

1. Either the one to its correct (lower-spring for the line)
2. One acme its correct and upwardly (upper-bound for the line)

The line is best approximated past those pixels that fall the least distance from the path between P_ane',P_ii'.

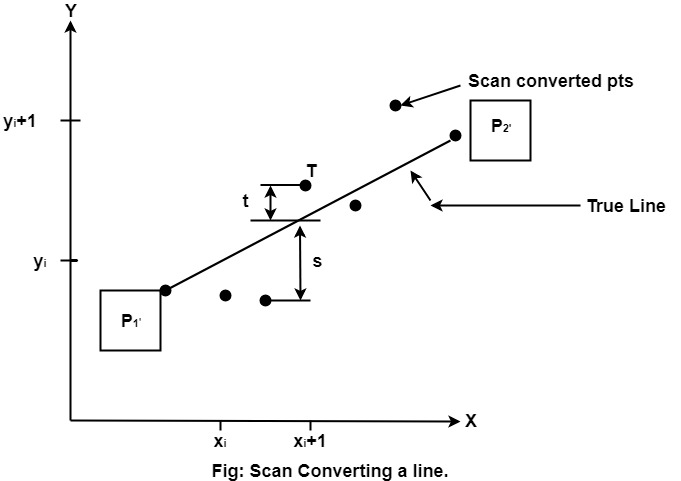
To chooses the adjacent one between the bottom pixel S and height pixel T.
If S is chosen
Nosotros have x_i+i=10_i+1       and       y_i+one=y_i
If T is chosen
Nosotros have x_i+1=ten_i+1       and       y_i+1=y_i+i

The bodily y coordinates of the line at x = x_i+1is
y=mx_i+1+b

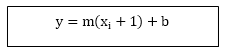
The altitude from S to the bodily line in y direction
s = y-y_i

The distance from T to the actual line in y management
t = (y_i+i)-y

At present consider the difference betwixt these 2 distance values
s - t

When (south-t) <0 ⟹ s < t

The closest pixel is S

When (southward-t) ≥0 ⟹ s < t

The closest pixel is T

This deviation is
southward-t = (y-yi)-[(yi+i)-y]
= 2y - 2yi -1

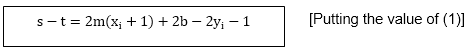
Substituting yard by 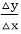and introducing decision variable
d_i=△x (s-t)
d_i=△10 (2 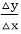(x_i+i)+2b-2y_i-1)
=2△xy_i-2△y-1△x.2b-2y_i△x-△x
d_i=2△y.ten_i-2△x.y_i+c

Where c= two△y+△x (2b-1)

We can write the decision variable d_i+1 for the side by side slip on
d_i+i=2△y.x_i+1-ii△10.y_i+1+c
d_i+i-d_i=two△y.(ten_i+1-10_i)- 2△x(y_i+1-y_i)

Since x_(i+1)=ten_i+1,we accept
d_i+1+d_i=2△y.(x_i+1-x_i)- 2△ten(y_i+ane-y_i)

Special Cases

If called pixel is at the top pixel T (i.e., d_i≥0)⟹ y_i+i=y_i+1
d_i+ane=d_i+2△y-2△x

If chosen pixel is at the bottom pixel T (i.due east., d_i<0)⟹ y_i+1=y_i
d_i+1=d_i+2△y

Finally, we calculate d₁
d₁=△x[2m(x₁+one)+2b-2y_ane-1]
d_one=△x[2(mx₁+b-y_i)+2m-1]

Since mx_one+b-y_i=0 and m = 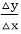, we accept
d₁=ii△y-△10

Advantage:

i. It involves only integer arithmetic, then information technology is simple.

ii. It avoids the generation of indistinguishable points.

3. Information technology tin be implemented using hardware because information technology does not use multiplication and partition.

4. It is faster as compared to DDA (Digital Differential Analyzer) because it does not involve floating point calculations like DDA Algorithm.

Disadvantage:

1. This algorithm is meant for basic line drawing only Initializing is not a function of Bresenham'south line algorithm. So to describe smooth lines, you lot should want to look into a different algorithm.

Bresenham'due south Line Algorithm:

Step1: Commencement Algorithm

Step2: Declare variable x₁,x₂,y_ane,y_ii,d,i₁,i_two,dx,dy

Step3: Enter value of x₁,y_one,x₂,y₂
Where x_i,y₁are coordinates of starting point
And x₂,y₂ are coordinates of Ending betoken

Step4: Calculate dx = x₂-x_ane
Calculate dy = y₂-y_one
Calculate i₁=2*dy
Summate i₂=ii*(dy-dx)
Calculate d=i_one-dx

Step5: Consider (ten, y) every bit starting point and x_endas maximum possible value of x.
If dx < 0
Then x = x_ii
y = y₂
x_finish=ten₁
If dx > 0
And then x = x₁
y = y_one
x_terminate=10₂

Step6: Generate point at (ten,y)coordinates.

Step7: Check if whole line is generated.
If x > = x_end
Stop.

Step8: Calculate co-ordinates of the next pixel
If d < 0
Then d = d + i₁
If d ≥ 0
Then d = d + i₂
Increase y = y + 1

Step9: Increment x = x + 1

Step10: Describe a point of latest (x, y) coordinates

Step11: Get to step 7

Step12: Cease of Algorithm

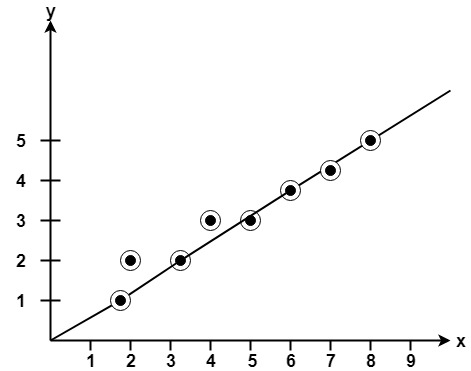
Example: Starting and Catastrophe position of the line are (i, 1) and (8, 5). Find intermediate points.

Solution: x₁=1
y₁=ane
x_two=8
y₂=5
dx= x₂-x₁=8-1=7
dy=y₂-y₁=5-1=4
I_ane=2* ∆y=two*four=8
I₂=2*(∆y-∆ten)=2*(four-7)=-6
d = I₁-∆x=eight-vii=i

x	y	d=d+Ii or I2
1	1	d+I2=1+(-half dozen)=-5
2	ii	d+I1=-v+8=iii
3	2	d+I2=3+(-6)=-three
4	iii	d+Iane=-3+eight=5
5	3	d+I2=5+(-vi)=-i
6	4	d+I1=-i+viii=7
7	4	d+Itwo=7+(-six)=1
8	five

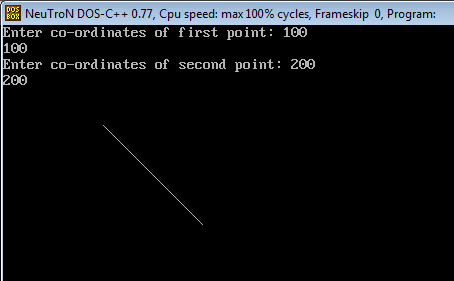
Programme to implement Bresenham'due south Line Cartoon Algorithm:

Output:

---

Differentiate betwixt DDA Algorithm and Bresenham's Line Algorithm:

DDA Algorithm	Bresenham's Line Algorithm
1. DDA Algorithm use floating point, i.e., Real Arithmetic.	one. Bresenham's Line Algorithm employ stock-still point, i.east., Integer Arithmetic
2. DDA Algorithms uses multiplication & division its operation	2.Bresenham'southward Line Algorithm uses simply subtraction and add-on its functioning
3. DDA Algorithm is slowly than Bresenham's Line Algorithm in line drawing because it uses real arithmetic (Floating Betoken operation)	3. Bresenham's Algorithm is faster than DDA Algorithm in line because information technology involves simply addition & subtraction in its adding and uses but integer arithmetic.
4. DDA Algorithm is non accurate and efficient as Bresenham's Line Algorithm.	4. Bresenham's Line Algorithm is more accurate and efficient at DDA Algorithm.
5.DDA Algorithm tin can draw circle and curves but are non accurate as Bresenham's Line Algorithm	5. Bresenham's Line Algorithm tin can draw circle and curves with more accurate than DDA Algorithm.

---

Adjacent Topic Defining a Circle

← prev next →

lambertyoullot.blogspot.com

Source: https://www.javatpoint.com/computer-graphics-bresenhams-line-algorithm

Share this post